2014年10月22日のNHKニュース巨大噴火 “今後100年間で確率約1%”によれば,「日本の広い範囲が火山灰で覆われ、火砕流が100キロ余り先まで達するような巨大噴火」が「今後100年間に起きる確率はおよそ1%で、回数にすると1万年に1回程度、阪神・淡路大震災を起こした兵庫県南部地震が起きる前の確率とほぼ同じ程度だということです」。
詳しくは神戸大学の巨大カルデラ噴火のメカニズムとリスクを発表にある(論文は Proceedings of the Japan Academy, Ser. B に出る予定らしい)。これによれば,兵庫県南部地震(阪神・淡路大震災)のほうは「発生前日における30年発生確率」である。地震調査研究推進本部の今までに公表した活断層及び海溝型地震の長期評価結果一覧の過去に発生した地震の、地震発生直前における確率によれば,30年確率は「0.02%〜8%」とのことである(このPDFが詳しい)。同程度といってもずいぶん幅があるようだ(30年と100年の違いどころではない)。
2011年の東日本大震災直後に話題になったが,その時点での東海地震の30年確率は87%であった(ウィキペディアの東海地震参照)。竹中平蔵氏の2011年5月10日のツイート「30年で大地震の確率は87%・・浜岡停止の最大の理由だ。確率計算のプロセスは不明だが、あえて単純計算すると、この1年で起こる確率は2.9%、この一カ月の確率は0.2%だ。原発停止の様々な社会経済的コストを試算するために1カ月かけても、その間に地震が起こる確率は極めて低いはずだ。」という計算が話題になった(竹中平蔵(笑) - Togetterまとめ 参照)。これに関連して書かれたブログをいくつか紹介する:
厳密には,地震発生確率は(一般的なPoissonモデルではなく)Brownian Passage Time(BPT)というモデルで計算されている(解説:地震発生確率の計算方法参照)。これは地震の周期が平均 $\mu$,分散 $(\alpha\mu)^2$ でじたばたするというモデルで,発生確率の密度関数は次で与えられる:
\[ f(t) = \sqrt{\frac{\mu}{2 \pi \alpha^2 t^3}} \exp \left(-\frac{(t - \mu)^2}{2 \alpha^2 \mu t} \right) \]ただし,東海地震については,前回の地震からの時間が平均周期をかなり超えているので,Poissonモデルで近似しても大きな違いはないであろう。
地震をPoisson過程と見るなら,1年間に地震の起こる確率 $p_1$ は一定で,地震発生は毎年独立であり,30年間地震が起こらない確率は $(1 - p_1)^{30}$ である。これを $1 - 0.87 = 0.13$ と等しいとおけば,$p_1 = 1 - 0.13^{1/30} = 0.066$ である:
> 1 - 0.13^(1/30)
[1] 0.0657464
この計算は上に挙げたブログの最初のものと同じである。
上に挙げた3番目のブログ記事では,この計算を「指数分布になるのに、二項分布を利用しているので計算結果が誤っている」と書いているが,これは勘違い。Poisson過程なら,任意の時点から次の地震が起こるまでの時間 $t$ の分布は
\[ f(t) = \lambda e^{- \lambda t} \]で与えられる指数分布になる。最初の1年に地震が起こる確率は
\[ p_1 = \lambda \int_0^1 e^{- \lambda t} dt = 1 - e^{- \lambda} \]同様に,30年間に地震が起こる確率は
\[ p_{30} = \lambda \int_0^{30} e^{- \lambda t} dt = 1 - e^{-30 \lambda} \]したがって
\[ p_1 = 1 - (e^{-30 \lambda})^{1/30} = 1 - (1 - p_{30})^{1/30} \]となる。つまり,「2項分布」を使っても指数分布を使っても同じことである。
いずれにしても,地震の確率なんてものは,ざっくりしたものなので,元の竹中氏の計算で十分という指摘ももっともである。
ちなみに,東海近辺で地震の起きた年をいくつか拾うと,
> x = c(1498, 1605, 1707, 1854)
> dx = diff(x)
> mean(dx)
[1] 118.6667
> sd(dx) / mean(dx)
[1] 0.2078462
> 2011 - x[4]
[1] 157
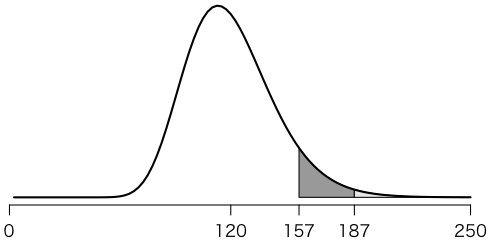
ということで,ざっくりと $\mu = 120$,$\alpha = 0.2$ でBPTモデルで計算すると,
> m = 120
> a = 0.2
> bpt = function(t) { (m/(2*pi*a^2*t^3))^(1/2)*exp(-(t-m)^2/(2*a^2*m*t)) }
> integrate(bpt, 157, 187)
0.06356807 with absolute error < 7.1e-16
> integrate(bpt, 157, Inf)
0.07306916 with absolute error < 9.1e-05
> 0.06356807 / 0.07306916
[1] 0.8699713
ということで,最新の地震から157年目の2011年から30年間に地震の起こる確率は87%になる。

plot(NULL, xlim=c(0,250), ylim=c(0,max(bpt(110:130))), axes=FALSE, xlab="", ylab="")
axis(1, c(0,120,157,187,250))
x = seq(157,187,5)
y = bpt(x)
polygon(c(x,x[length(x)],x[1]), c(y,0,0), col=gray(0.6))
x = seq(187,250,7)
y = bpt(x)
polygon(c(x,x[length(x)],x[1]), c(y,0,0), col=gray(0.9))
curve(bpt(x), lwd=2, add=TRUE)
同様に,最初の1年では
> integrate(bpt, 157, 158)
0.004361829 with absolute error < 4.8e-17
> 0.004361829 / 0.07306916
[1] 0.05969453
で,5.97%となる。「30年確率は87%」のPoissonモデルで計算した6.57%より少し小さい。
ちなみに,$\lambda \int_0^{\infty} t e^{-\lambda t} dt = 1/\lambda$ であるので,$\lambda$ は次の地震が起きるまでの時間の期待値の逆数である。東海地震の平均間隔を120年として $\lambda = 1/120$ の指数分布であてはめてみれば,いつを起点としても30年確率は $(1/120) \int_0^{30} e^{-t/120} dt = 0.22$ であり,BPTモデルとまったく異なる。
Last modified: