裏 RjpWiki の 2 個の時系列データの相関を考えるときは... と 2 個の時系列データの相関を考えるときは...(その2) がたいへんおもしろかったので試してみた。
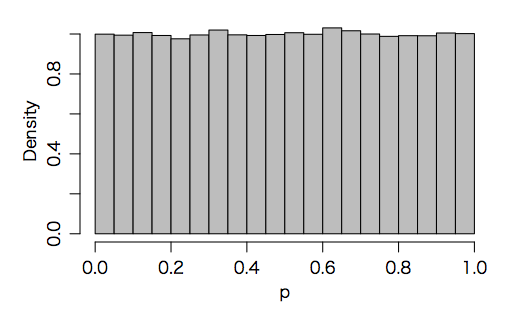
まず p 値は本来は帰無仮説のもとに一様分布になるべきである。例:
p = replicate(100000, {
x = rnorm(100)
y = rnorm(100)
cor.test(x, y)$p.value
})
hist(p, freq=FALSE, breaks=20, col="gray", main="")

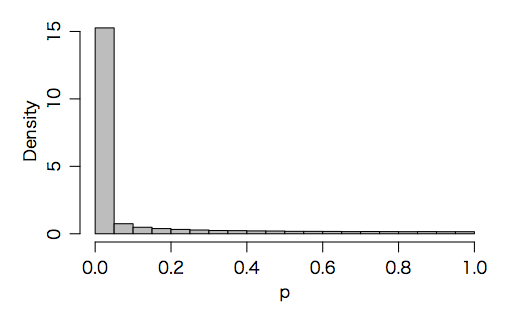
しかし「時系列」ではそうならないことがある。例として,まったく独立に生成されたはずの二つのランダムウォークする系列の相関係数を求めると,こんな具合になる:
p = replicate(100000, {
x = cumsum(rnorm(100))
y = cumsum(rnorm(100))
cor.test(x, y)$p.value
})
hist(p, freq=FALSE, breaks=20, col="gray", main="")
こういう場合には,「時間」t = 1:100 の影響を引いた偏相関係数を使えばよい(?)。偏相関係数とその p 値を求める関数は,裏RjpWikiのコードを借用して作った:
pcor = function(x, y, t) {
r_xy = cor(x, y) # 単相関係数
r_tx = cor(t, x) # 時間との単相関係数
r_ty = cor(t, y) # 時間との単相関係数
r_xy.t = (r_xy-r_tx*r_ty)/sqrt(1-r_tx^2)/sqrt(1-r_ty^2) # 偏相関係数
n = length(t)
t.stat = abs(r_xy.t)*sqrt(n-3)/sqrt(1-r_xy.t^2) # 母偏相関係数=0 の検定統計量
p.value = pt(t.stat, df=n-3, lower.tail=FALSE)*2 # P 値を求める(両側検定)
c(r_xy.t, p.value)
}
p = replicate(100000, {
x = cumsum(rnorm(100))
y = cumsum(rnorm(100))
t = 1:100
pcor(x, y, t)[2]
})
hist(p, freq=FALSE, breaks=20, col="gray", main="")
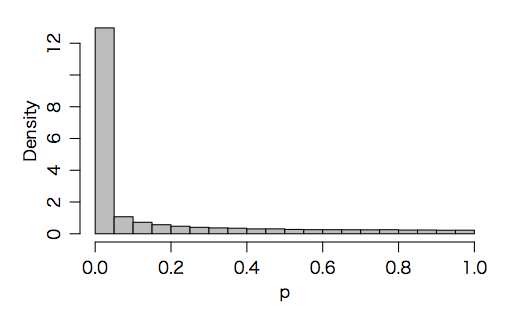
あれ,「時間」の影響を引いてもやっぱりおかしい。
念のため
2 個の時系列データの相関を考えるときは...(その2)
にあるサンプルデータ d でやってみると
> pcor(d$x, d$y, d$t)
[1] -0.1263188 0.4435144
で一致するので pcor() のバグではないと思う。
ちなみに,偏相関係数を求めるには ppcor というパッケージの pcor(),pcor.test() があるようなので,使ってみる:
> library(ppcor)
> pcor.test(d$x, d$y, d$t)
estimate p.value statistic n gp Method
1 -0.1263188 0.4385926 -0.7745721 40 1 pearson
偏相関係数そのものは一致するが p 値は少し違う。どうやらこれは pt() でなく pnorm() を使って p 値を求めているようだ。念のためこちらの p 値を使っても同様な結果が得られた。
結論:「時系列」(ランダムウォーク)データの「見せかけの回帰」(spurious regression)は,時間の(線形な)影響を引き去った偏相関係数を使っても,依然として存在する。
なお,偏相関係数の p 値は,線形回帰 summary(lm(d$y ~ d$x + d$t)) の d$x の係数の p 値と等しい。こちらは t 検定を使っている。
[2014-09-24] 相関係数の p 値と偏相関係数の p 値の関係も調べてみた。
p = replicate(1000, {
x = cumsum(rnorm(100))
y = cumsum(rnorm(100))
t = 1:100
c(cor.test(x, y)$p.value, pcor(x, y, t)[2])
})
plot(p[1,], p[2,], asp=1, xlab="相関係数のp値", ylab="偏相関係数のp値",
xlim=c(0,1), ylim=c(0,1))
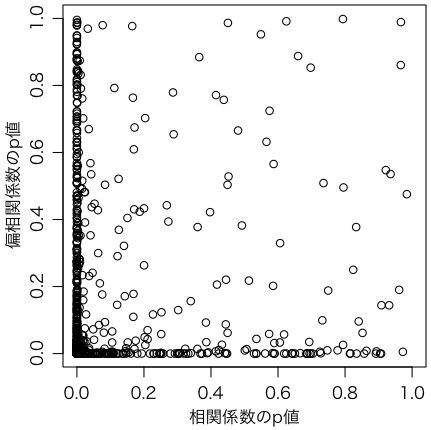
p = replicate(100000, {
x = cumsum(rnorm(100))
y = cumsum(rnorm(100))
t = 1:100
c(cor.test(x, y)$p.value, pcor(x, y, t)[2])
})
cor(p[1,], p[2,])
両 p 値の相関係数は 0.09 程度で,弱い相関しかない。有意な相関係数があっても,偏相関係数にすることによって有意でなくすことができるかもしれないが,その逆もありうる。
Last modified: