TALIS - The OECD Teaching and Learning International Survey のデータを R で読んで解析する手順は,りん先生の RでTALIS2018 に書かれている通りである。ここでは Python で同じことをやってみる。
pandas の IO Tools のページにいろいろなファイルの読み方が書いてあるが,SPSS のファイルについては書かれていない。書いてないだけで,read_spss() という関数があるが,それは pyreadstat パッケージを使っているだけである。ここでは pyreadstat を直接使うことにする。これは R の haven パッケージと同程度に高速である。試しに中学校のデータを読んでみる:
import pyreadstat
df, meta = pyreadstat.read_sav("BTGINTT3.sav")
これで df に 153682 行 397 列のデータが,meta にメタデータが入る。メタデータには次のものがある:
meta.column_labels meta.column_names meta.file_encoding
meta.file_format meta.file_label meta.missing_ranges
meta.missing_user_values meta.notes meta.number_columns
meta.number_rows meta.original_variable_types meta.table_name
meta.value_labels meta.variable_alignment meta.variable_display_width
meta.variable_measure meta.variable_storage_width meta.variable_to_label
meta.variable_value_labels
国別の行数は次のようにして求められる:
df['CNTRY'].value_counts()
日本(JPN)は 3555 件ある。
例えばアンケート 34. In your teaching, to what extent can you do the following? の中の m) Support student learning through the use of digital technology (e.g. computers, tablets, smart boards) の回答(1 = Not at all, 2 = To some extent, 3 = Quite a bit, 4 = A lot)については df['TT3G34M'] にある。この度数分布は df['TT3G34M'].value_counts() で求められる。日本に限定した度数分布は
df['TT3G34M'][df['CNTRY'] == 'JPN'].value_counts()
で求められる。
データを国で分類し,上記アンケート結果の平均を求め,昇順に並べ,NaN でないものだけを残す:
s = df.groupby('CNTRY')['TT3G34M'].mean()
s.sort_values(inplace=True)
s = s[s.notna()]
とりあえず簡単な棒グラフで表す:
import matplotlib.pyplot as plt
plt.figure(figsize=[6.4, 9])
plt.barh(s.index, s)
plt.xlim(1, 4)
ドットプロットにしてみる:
plt.plot(s, s.index, "o")
plt.grid()
plt.xlim(1, 4)
国名を日本語にするには,次のようにすればよい:
co = pd.read_csv("https://okumuralab.org/~okumura/stat/data/countries.csv")
dic = { r['三字']: r['国名'] for i,r in co.iterrows() }
cj = [ dic[x] for x in s.index ]
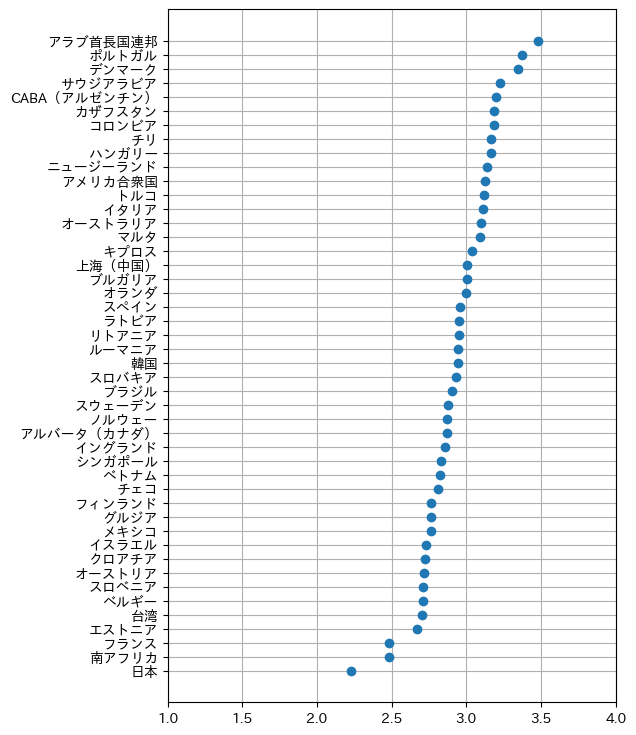
plt.plot(s, cj, "o")
plt.subplots_adjust(left=0.25, right=0.95)
plt.grid()
plt.xlim(1, 4)
plt.savefig('190707a.png', bbox_inches="tight")

要するに日本は「デジタル技術を使って生徒の学びをサポートする」(Support student learning through the use of digital technology)で最低点であるということだ。
Last modified: