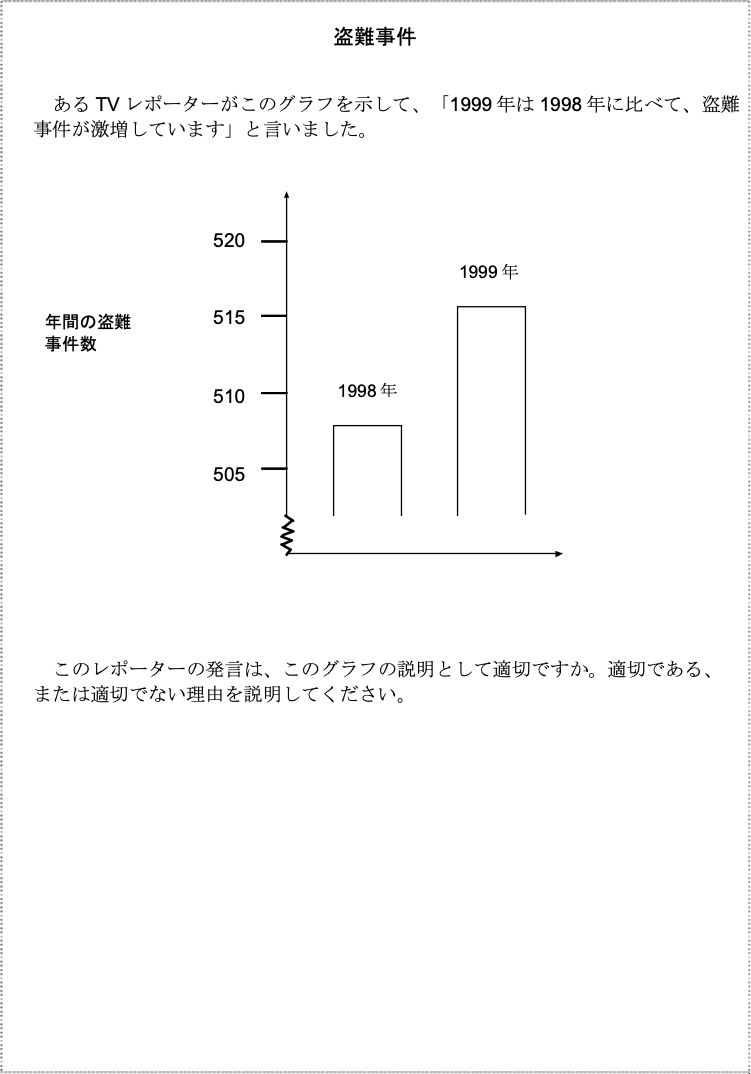
PISA「盗難事件」問題でも書きましたが,昔PISAにこんな問題がありました:

グラフから数値を読み取ると,それぞれ508,516,合わせて1024です。
「激増している」の反対は「たいして変わらない」です。これを「1999年も1998年も盗難事件の起こる確率は同じ」というふうに言い換えて,モデル化してみましょう。
1024件の事件がそれぞれ同じ確率で1998年・1999年に起きるということは,0・1 の乱数を1024個作ることでモデル化できます。
import numpy as np rng = np.random.default_rng() # 乱数生成器(random number generator)を作る rng.integers(0, 2, size=1024) # 0以上2未満の整数1024個
1999年に起きる事件の数は,1 の出る回数です。
sum(rng.integers(0, 2, size=1024))
これが516以上である確率を求めてみましょう。
N = 10000
s = 0
for i in range(N):
if sum(rng.integers(0, 2, size=1024)) >= 516:
s = s + 1
print(s / N)
同じことは次のように書くこともできます:
x = np.array([sum(rng.integers(0, 2, size=1024)) for _ in range(10000)]) sum(x >= 516) / len(x)
ついでにヒストグラム:
import matplotlib.pyplot as plt plt.hist(x, bins=range(512-64, 512+64, 4), edgecolor="black")
516以上だけ色を変えてみましょう。
plt.hist(x[x < 516], bins=range(512-64, 512+64, 4), color="C0", edgecolor="black") plt.hist(x[x >= 516], bins=range(512-64, 512+64, 4), color="C1", edgecolor="black")
1999年の事件が516件以上起きる確率は4割以上あることがわかるでしょう。つまり,どちらの年に事件が起きる確率も同じと仮定しても,こういうことはよく起きるので,「激増」とは言えなさそうです。
ここで仮定した「どちらの年も同じ」という仮定を「帰無仮説」といいます。帰無仮説を仮定して,現実またはそれ以上の差が生じる確率を,「p 値」(p-value)といいます。p 値があらかじめ決めた値(有意水準、例えば 0.05)より小さければ,偶然とは考えられないほどの違いがあると考えます。
上で述べたことは,2022年から学年進行で高校で教えられる「数学I」の「データの分析」で「具体的な事象において仮説検定の考え方を理解すること」と書かれていることに関連します。より高度な内容は同じく「数学B」で扱われます。学習指導要領から「数学B」の該当部分を引用しておきます:
(2) 統計的な推測
統計的な推測について,数学的活動を通して,その有用性を認識するとともに,次の事項を身に付けることができるよう指導する。
ア 次のような知識及び技能を身に付けること。
(ア) 標本調査の考え方について理解を深めること。
(イ) 確率変数と確率分布について理解すること。
(ウ) 二項分布と正規分布の性質や特徴について理解すること。
(エ) 正規分布を用いた区間推定及び仮説検定の方法を理解すること。
イ 次のような思考力,判断力,表現力等を身に付けること。
(ア) 確率分布や標本分布の特徴を,確率変数の平均,分散,標準偏差などを用いて考察すること。
(イ) 目的に応じて標本調査を設計し,収集したデータを基にコンピュータなどの情報機器を用いて処理するなどして,母集団の特徴や傾向を推測し判断するとともに,標本調査の方法や結果を批判的に考察すること。
[用語・記号]信頼区間,有意水準