mpmath(mpmath.org)は Python の任意精度浮動小数点演算パッケージです。
pip install mpmath でインストールできます。
デフォルトでは Python の整数演算を使います:
import mpmath.libmp mpmath.libmp.BACKEND
'python'
可能なら、多倍長演算パッケージ gmpy2(ドキュメント)をインストールすると、高速な計算ができます:
pip install gmpy2
mpmath のバックエンドが変わったか確かめます:
import mpmath.libmp mpmath.libmp.BACKEND
'gmpy'
計算の準備と精度の確認:
from mpmath import mp print(mp)
Mpmath settings: mp.prec = 53 [default: 53] mp.dps = 15 [default: 15] mp.trap_complex = False [default: False]
mp.prec は2進精度、mp.dps は10進精度(decimal places)です。10進50桁精度に変えてみましょう:
mp.dps = 50 print(mp)
Mpmath settings: mp.prec = 169 [default: 53] mp.dps = 50 [default: 15] mp.trap_complex = False [default: False]
簡単な例として $\int_{-\infty}^{\infty} \exp(-x^2) dx = \sqrt{\pi}$ を使って円周率を求めてみましょう:
mp.pretty = True mp.quad(lambda x: mp.exp(-x**2), [-mp.inf, mp.inf]) ** 2
3.1415926535897932384626433832795028841971693993751
デフォルト mp.pretty = False では print() を付けないときれいな数値表現になりません。mp.pretty = True にしておくほうが便利です。
mpmath を調べ始めた動機は、NHK特集リーマン予想を見て、リーマンのゼータ関数のゼロ点を Python で簡単にプロットできないかと思ったからでした。
Python では SciPy にもゼータ関数はありますが、実数だけです。mpmath には複素数のゼータ関数が含まれています。
うまくゼロ点を見せる方法があればいいのですけれど、とりあえず:
import matplotlib.pyplot as plt
import numpy as np
from mpmath import zeta
def logzeta(z):
return np.log10(float(abs(zeta(z))))
vlogzeta = np.vectorize(logzeta)
x, y = np.meshgrid(np.linspace(-30, 30, 600), np.linspace(-30, 30, 600))
z = vlogzeta(x + y * 1j)
plt.figure(figsize=(6, 6))
plt.pcolormesh(x, y, z, cmap='gray', vmin=-3, vmax=0)
plt.axis('scaled')

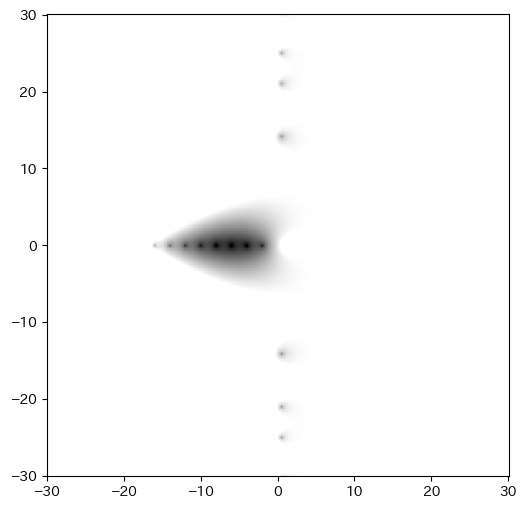
横に並んでいるのが自明なゼロ点、縦に並んでいるのが非自明なゼロ点です。
Last modified: