
高等学校情報科「情報Ⅰ」教員研修用教材(本編)の「第3章 コンピュータとプログラミング」の乱数を使ったシミュレーション(p.138〜)についてコメントします。
まず、Python での乱数の作り方:

このように乱数を1個ずつ生成するのなら標準ライブラリ random の乱数で十分ですが、ここでは次に使う NumPy の導入にしたかったのでしょう。
ちなみに、NumPy を使うなら、乱数のページでも説明しましたが、2013年にリリースされた NumPy 1.17.0 からは Generator を使った新しいインターフェースが推奨されています:
import numpy as np
rng = np.random.default_rng()
ransuu = rng.random()
print("乱数", ransuu)
このように rng = np.random.default_rng() を引数なしで呼ぶと毎回ランダムに初期化されますが、一般的な使い方としては、あとで同じシミュレーションが再現できるように、例えば rng = np.random.default_rng(12345) のように任意の整数値をタネ(seed)として与えます。授業なら、出席番号(学籍番号)をタネにするのもいいかもしれません。
次はさいころを100回振るプログラム:

とりあえず NumPy の新しい方式に直して、PEP 8 に合わせて少し書き直します:
import numpy as np
rng = np.random.default_rng()
saikoro = rng.integers(1, 6 + 1, size=100)
print(saikoro)
deme = []
for i in range(6):
deme.append(np.count_nonzero(saikoro == i + 1))
print("出現数:", deme)
np.count_nonzero() は、np.sum() や、単なる sum() でもかまいません(この場合は np.count_nonzero() が最も速く、次に np.sum() が速いようです)。
deme = [] から始まる3行は次のようにもできます:
deme = [np.count_nonzero(saikoro == i + 1) for i in range(6)]
さて、度数分布図:

これはこれで問題ありませんが、align="center" はデフォルトなので省いて、少し整理しました:
import matplotlib.pyplot as plt import numpy as np rng = np.random.default_rng() saikoro = rng.integers(1, 6 + 1, size=100) x, deme = np.unique(saikoro, return_counts=True) plt.bar(x, deme)
E.V.ジュニアさん(現在のペンネームはクリヤキンさん)のnoteでは、分類してから棒グラフを描くのではなく、最初から度数分布図を描いています:
plt.hist(saikoro, bins=np.arange(0.5, 7.5), rwidth=0.8)
次はモンテカルロ法で円周率を求めるプログラム:
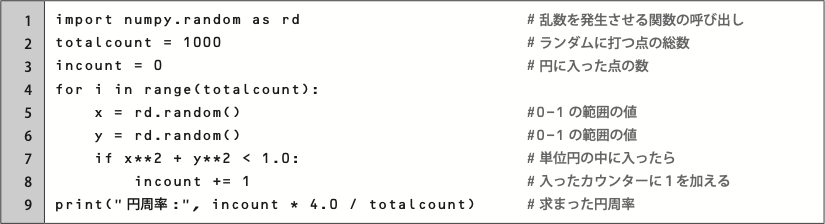
Generator を用いる方式にして、ループをベクトル化すると、次のようになります:
import numpy as np
rng = np.random.default_rng()
totalcount = 1000
x = rng.random(totalcount)
y = rng.random(totalcount)
incount = np.count_nonzero(x**2 + y**2 < 1)
print("円周率:", incount * 4 / totalcount)
散布図を描くプログラム:

このように plt.scatter() を点ごとに呼び出すのはたいへん能率が悪い方法です。次のようにしてはどうでしょうか:
import matplotlib.pyplot as plt
import numpy as np
rng = np.random.default_rng()
totalcount = 2000
x = rng.random(totalcount)
y = rng.random(totalcount)
c = x*x + y*y < 1
plt.scatter(x, y, c=c)
plt.axis('scaled') # これをしないとアスペクト比が1にならない
色を選ぶ方法はいろいろ考えられそうです。パレットをいじらずに済ませる方法:
col = ['red' if i else 'blue' for i in c] plt.scatter(x, y, color=col)
別解
plt.scatter(x[c], y[c], color="red") plt.scatter(x[np.logical_not(c)], y[np.logical_not(c)], color="blue") # または plt.scatter(x[~c], y[~c], color="blue")
seaborn を使う例(デフォルトでうまい具合の色になる):
import seaborn as sns sns.scatterplot(x=x, y=y, hue=c)
ちなみに、文科省の研修用教材には他プログラミング言語版としてJavaScript版、VBA版、ドリトル版、swift版(なぜかSwiftだけ全角文字で小文字で始まっている)がありますが、2019年11月21日に出たVBA版では次のようになっていました:

実行結果は次の通り:
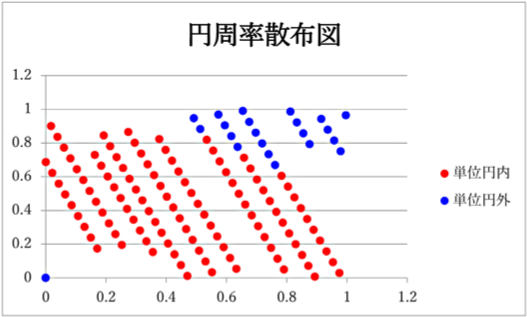
これを見ればバグっていることは自明です。ちなみにツイッターで騒がれたせいか、2019年12月11日にはリンク切れとなり、12月27日には修正版が出ました。