政党0，1，2，3がそれぞれ1000，650，200，150票を得た。10人当選させるには，各政党から何人ずつ選べばよいか。
import numpy as np
r = 10 # 当選数
n = a = np.array([1000, 650, 200, 150]) # 得票数
for i in range(2, r + 1):
a = np.append(a, n / i)
a
array([1000. , 650. , 200. , 150. ,
500. , 325. , 100. , 75. ,
333.33333333, 216.66666667, 66.66666667, 50. ,
250. , 162.5 , 50. , 37.5 ,
200. , 130. , 40. , 30. ,
166.66666667, 108.33333333, 33.33333333, 25. ,
142.85714286, 92.85714286, 28.57142857, 21.42857143,
125. , 81.25 , 25. , 18.75 ,
111.11111111, 72.22222222, 22.22222222, 16.66666667,
100. , 65. , 20. , 15. ])
この上位 r 人を選べばよい。
o = np.argsort(-a) np.bincount((o % 4)[:r])
array([6, 3, 1])
この場合，最後の 0 は出力されない。なお，タイがない（a[o][r-1] と a[o][r] が等しくない）ことも確認しなければならない。
別解：
r = 10 # 当選数
n = np.array([1000, 650, 200, 150]) # 得票数
h = np.zeros_like(n) # 配分（最初はすべて0）
for _ in range(r):
a = n / (h + 1)
h[np.argmax(a)] += 1
h
array([6, 3, 1, 0])
この場合，タイを検出するには，最後の np.argmax(a) が一意であることを示せばよい。例えば：
if np.argmax(a) != len(a) - 1 - np.argmax(a[::-1]):
print("タイです")
あるいは
i, = (a == a.max()).nonzero()
if len(i) > 1:
print("タイ:", i)
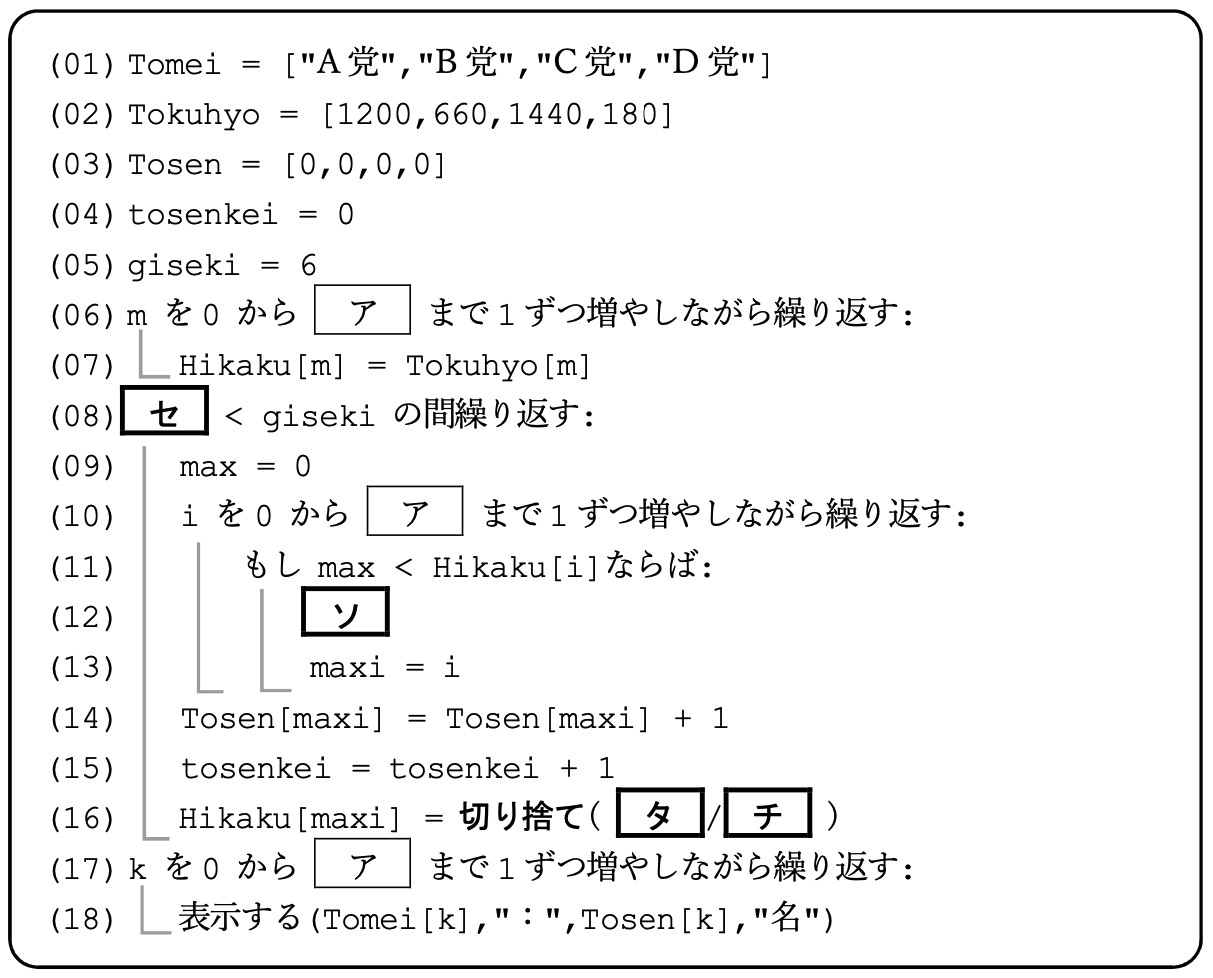
この問題が，大学入試センター共通テストで2025年から出題される予定の「情報I」のサンプル問題（2021-03-24）に出題された：
こういう日本語の擬似言語を大学入試センターではDNCL（Daigaku Nyushi Center Language）と呼んでいたが、令和７年度試験の問題作成の方向性、試作問題等の「概要「情報」」では「共通テスト用プログラム表記」という呼称に統一されたようである。
これをPythonに直すと次のようになる。配列名は「共通テスト用プログラム表記」では大文字で始める約束のようだが，Pythonでは大文字で始めるとクラス名のように見えるので，ここでは小文字にした。擬似言語なので，上の (06)，(07) のような書き方でもエラーにならないが，Pythonはあらかじめ配列を確保しておかなければならない（Pythonがよくわかっていればこの部分は hikaku = tokuhyo.copy() と書くであろう）。
tomei = ["A党", "B党", "C党", "D党"]
tokuhyo = [1200, 660, 1440, 180]
tosen = [0, 0, 0, 0]
tosenkei = 0
giseki = 6
hikaku = [0, 0, 0, 0] # これがないとエラーになる
for m in range(4):
hikaku[m] = tokuhyo[m]
while tosenkei < giseki:
max = 0
for i in range(4):
if max < hikaku[i]:
max = hikaku[i]
maxi = i
tosen[maxi] = tosen[maxi] + 1
tosenkei = tosenkei + 1
hikaku[maxi] = int(tokuhyo[maxi] / (tosen[maxi] + 1))
for k in range(4):
print(tomei[k], ":", tosen[k], "名")
こちらは商を切り捨てて整数にしている（int(tokuhyo[maxi] / (tosen[maxi] + 1)) または tokuhyo[maxi] // (tosen[maxi] + 1)）ので，最初のアルゴリズムと若干答えが違ってくるかもしれない。
ドント方式は公職選挙法で次のように定められている：
第九十五条の二 衆議院（比例代表選出）議員の選挙においては、各衆議院名簿届出政党等の得票数を一から当該衆議院名簿届出政党等に係る衆議院名簿登載者（当該選挙の期日において公職の候補者たる者に限る。第百三条第四項を除き、以下この章及び次章において同じ。）の数に相当する数までの各整数で順次除して得たすべての商のうち、その数値の最も大きいものから順次に数えて当該選挙において選挙すべき議員の数に相当する数になるまでにある商で各衆議院名簿届出政党等の得票数に係るものの個数をもつて、それぞれの衆議院名簿届出政党等の当選人の数とする。
２ 前項の場合において、二以上の商が同一の数値であるため同項の規定によつてはそれぞれの衆議院名簿届出政党等に係る当選人の数を定めることができないときは、それらの商のうち、当該選挙において選挙すべき議員の数に相当する数になるまでにあるべき商を、選挙会において、選挙長がくじで定める。
３〜６ 略
第九十五条の三 参議院（比例代表選出）議員の選挙においては、各参議院名簿届出政党等の得票数（当該参議院名簿届出政党等に係る各参議院名簿登載者（当該選挙の期日において公職の候補者たる者に限る。第百三条第四項を除き、以下この章及び次章において同じ。）の得票数を含むものをいう。）を一から当該参議院名簿届出政党等に係る参議院名簿登載者の数に相当する数までの各整数で順次除して得たすべての商のうち、その数値の最も大きいものから順次に数えて当該選挙において選挙すべき議員の数に相当する数になるまでにある商で各参議院名簿届出政党等の得票数（当該参議院名簿届出政党等に係る各参議院名簿登載者の得票数を含むものをいう。）に係るものの個数をもつて、それぞれの参議院名簿届出政党等の当選人の数とする。
２ 前項の場合において、二以上の商が同一の数値であるため同項の規定によつてはそれぞれの参議院名簿届出政党等に係る当選人の数を定めることができないときは、それらの商のうち、当該選挙において選挙すべき議員の数に相当する数になるまでにあるべき商を、選挙会において、選挙長がくじで定める。
３〜５ 略
商を整数に切り捨てるのかどうかは書かれていない。ただ，解説してあるページはどれも切り捨ててないようだし，切り捨てる意味もなさそうなので，サンプル問題の間違い（というほどでもないが）のように思う。
アダムズ方式も参照されたい。
Last modified: