1937年にドイツの数学者Collatz(コラッツ)が、「ある数が偶数なら2で割り、奇数なら3倍して1を足す。これを繰り返すとすべての数は1になるだろう」と予想しましたが、だれもそれを証明することができていません(ウィキペディアのコラッツの問題参照)。証明できたら1億2000万円もらえるそうです。
Pythonのプログラムで調べてみましょう。
def collatz(n):
print(n, end="")
while (n > 1):
if (n % 2 == 0):
n = n // 2
else:
n = 3 * n + 1
print(" →", n, end="")
print()
ここで n % 2 はnを2で割った余りです。
例えば collatz(3) と打つと次のように出ます。
3 → 10 → 5 → 16 → 8 → 4 → 2 → 1
いろいろな数から出発して、Collatzの予想が正しいかどうか確かめてください。Pythonの整数はどんな大きな数でも扱えますので、桁あふれする心配はありません。
なお、n = n // 2 は n //= 2 と書くこともできます。同様に、n = n + 1 は n += 1 と書けます。
n // 2 は n を2で割った整数の商を求めます。ここでは n は偶数ですので、単に n / 2 としてもかまいません。ただ、n / 2 だと浮動小数点の割り算になり,n が非常に大きい場合にうまくいかない可能性があります。Python は整数についてはどんなに大きな値でも正確に計算します(メモリに入る限り)。
n = n + 1 と n += 1 では、前者は n を2回評価し、後者は n を1回しか評価しないという違いがあります。評価することによって副作用が生じる場合は、結果が違うことがありますが、上のような単純な例では、まったく違いがないと考えて差し支えありません。n += 1 のほうが必ずしも実行が速いというわけでもありません。
入力を促すためには次のようにします:
n = int(input("正の整数を入力してください: "))
collatz(n)
関数 input() はキーボード入力を文字列として読み込みます。整数にしたいときは int()、浮動小数点数にしたいときは float() で変換します。
Collatz の問題で、最後は 1 になるとしても、途中でどれくらい大きい数になるでしょうか。これを調べるための関数を作ってみましょう:
def collatz_max(n):
nmax = n
while (n > 1):
if (n % 2 == 0):
n = n // 2
else:
n = 3 * n + 1
if n > nmax:
nmax = n
return nmax
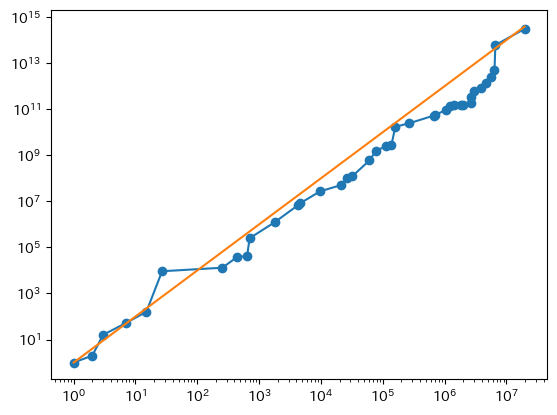
これは n が大きくなるにつれてどれくらい大きくなるでしょうか。
mmax = 0
for n in range(10000):
m = collatz(n)
if m > mmax:
print(n, m)
mmax = m
range() の数をもっと大きくしてやってみましょう。

オレンジの線は n の2乗を表します。