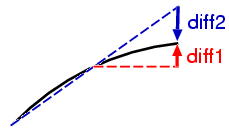
差分
diff1i = origi - origi-1
2階差分
diff2i = diff1i - diff1i-1 = origi - 2 origi-1 + origi-2

例として

の線分 (108, 0) -- (108, 255) を考える。
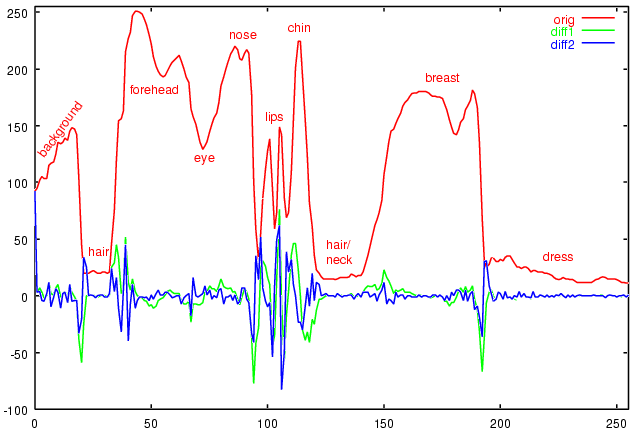
エントロピー
Entropy = Σ p log2 (1 / p)
を計算してみる。
| orig | 6.62867 |
| diff1 | 4.77229 |
| diff2 | 4.45207 |
| x(i-1,j-1) | x(i-1,j) |
| x(i,j-1) | x(i,j) |
3点を通る平面で予測
x(i,j)の予測値 = x(i,j-1) + x(i-1,j) - x(i-1,j-1)
Lisa データで予測誤差のエントロピーは 3.39197
ただし,外挿は時として危険なので,ある範囲 (たとえば x(i,j-1),x(i-1,j),x(i-1,j-1) の最小値と最大値の間) から外れないようにする。
この修正を取り入れた場合,エントロピーは 3.28226
x(i,j,k)の予測値 =
(x(i,j,k-1) - x(i,j-1,k-1)) - (x(i-1,j,k-1) - x(i-1,j-1,k-1))
+ (x(i-1,j,k) - x(i-1,j-1,k)) + x(i,j-1,k)
ただし,たとえば i,j が空間座標で k が時間座標といった場合, i,j と k が同じ重みで効くとは限らない。
x(i,j,k)の予測値 =
重み×((x(i,j,k-1) - x(i,j-1,k-1)) - (x(i-1,j,k-1) - x(i-1,j-1,k-1)))
+ (x(i-1,j,k) - x(i-1,j-1,k)) + x(i,j-1,k)
Last modified: 2004-05-26 16:48:34